Define
A graph consists of a set of nodes V and a set of edges E.
- Each edge in E joins two nodes in V
- Two nodes connected by an edge are called neighbors or adjacent
Edge
- undirected: can be traversed in both directions
{x,y},edge xy: When there is only one edge connecting two nodes x and y
simple graph
the graph which has neither multiple edges nor loop edges
Degrees
the degree of a node v is the number of edges which have v as an endpoint. Represent by Deg(v)
- if self loop, count twice
For example,deg(a)= 2,deg(b)= 6,deg(d)= 0
The relation between edge number and degree is
$$ \sum_{v\in V}deg(v)=2|E| $$
Type of graph
Several special types of graphs that are useful
1. Complete graph
every node is connected to every other node,l represent by $K_i$ where i represent the node number
the above complete graph is $K_5$
the edge of it equal to:
$$ \text{edge} = \frac{n(n-1)}{2} $$
2. Cycle graphs
all nodes and edges connecting vi to vi+1, plus an additional edge from vn to v1. where as v represent each single nodes in the graph.
the above cycle graph is $C_5$
$$ \text{edge}= n $$
- the cycle graph $C_n$ contains 2n different cycles (different start)
3. Wheel
cycle + an external hub, represent by $W_i$ where i is the node number - 1
the above wheel represent by $W_5$
- $W_n$ has $n+1$ node
$$ \text{egde}=2n $$
Isomorphism
Suppose $G(V_1,E_1)$ and $G_2(V_2,E_2)$ are graphs, an isomorphism means $G_1$ to $G_2$ is a bijection $f : V_1 \to V_2$
if there is an isomorphism from $G_1$ to $G_2$, then, we can say they are isomorphic
the above graph is isomorphic because we can map 1 to d, 2 to a, 3 to c and 4 to d
- isomorphism is another example of an equivalence relation
Check NOT isomorphism:
If not satisfied:
- same number of nodes and the same number of edges.
- same number of nodes of degree k
If the two property are identical, we should notice on their subspace. If two graphs G and F are isomorphic, then any subgraph of G must have a matching subgraph somewhere in F.
Subspace: If G and G′ are graphs, then G′ is a subgraph of G if and only if the nodes of G′ are a subset of the nodes of G and the edges of G′ are a subset of the edges of G
the left graph has $C_3$ as a subspace but right graph does not.
Walks, paths, and cycles
Walk: sequence of node or edge from one node to another node
- shortest walk is zero (single node)
- the walk is closed if its start and end are the same, otherwise it's open
- can be more than one
Path: a walk in which no node is used more than once
- cycle is a closed walk with at least three nodes in which no node is used more than once except that the starting and ending nodes are the same
- cycle diff from close walk that close walk can re-use node
- acyclic means does not contain cycle in graph
- can create a path between the nodes by pruning unnecessary loops from the walk.
- can be more than one
Distances
distance from a to b means the length of the shortest path from a to b
- diameter of a graph is the max distance between any pairs of nodes
diameter above is 4 since $d(f,e)=4$
Connectivity
A graph G is connected if there is a walk between every pair of nodes in G
Not connected because no walk from a to g
connected components: some subset in a graph that each contains a maximal set of nodes that are all connected to one another. The graph above has three connected components
cut edge: if a connected graph become disconnected by removing a single edge, this edge is cut edge
Euler circuits
a closed walk that uses each edge of the graph exactly once
Check is Euler circuits
- the graph is connected
- each node has even degree
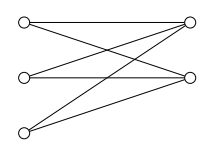
Bipartite graphs
A graph G = (V, E) is bipartite if we can split V into two non-overlapping subsets V1 and V2 such that every edge in G connects an element of V1 with an element of V2
all R and all G nodes in this graph is not connected with themselves, but connect with each other,o so, it is bipartite graph
Complete bipartite graph:
- bipartite graph + each subsets are completed connected
- represent by $K_{m,n}$ where m and n represent node in each subsets
complete bipartite graph: $K_{3,2}$
$$ \text{node}=m+n $$
$$ \text{edge}=mn $$