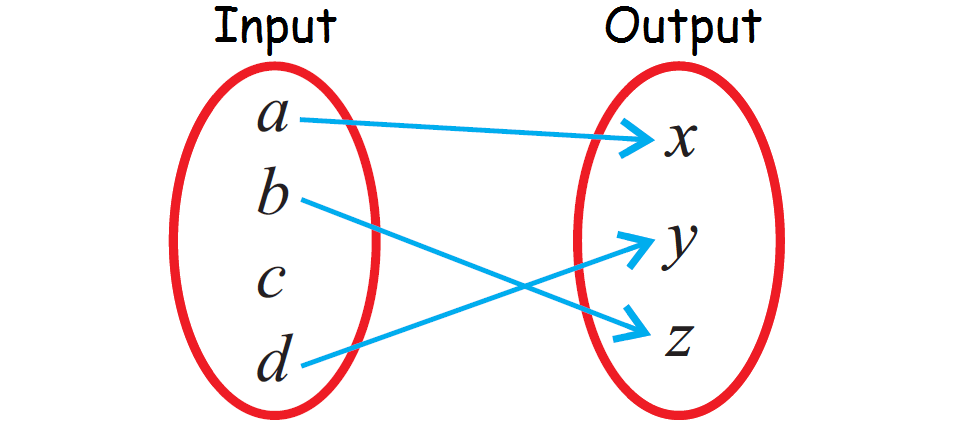
- input and/or output values may be integers, strings, characters...
- represent by $f : A → B$, where as A is domain (input) and B is co-domain. f(x) is called image
- For each input value, a function must provide one and only one output value
Identity function: represent by $iD_A$, $iD_A : A → A$
Equal
To be equal, two functions must (obviously) assign the same output value to each input value. But, in addition, they must have the same type signature.
they are different functions since they have different signature even if equation is the same
f : N → N such that f(x) = 2x.
f : R → R such that f(x) = 2x
they are the same functions since they have same signature and same input corresponding to the same output even if equation is not the same
f : Z → Z such that f(x) = |x|.
f : Z → Z such that f(x) = max(x, −x).
f : Z → Z such that f(x) = x if x ≥ 0 and f(x) = −x if x ≤ 0.
Image and Onto
Image: for the function f : A → B, image is the set of values produced when f is applied to all elements of A. Represent by f(A)
$$ f(A) = {f(x) : x ∈ A} $$
Onto: f : A → B is onto if its image is its whole co-domain
$$ ∀y ∈ B, ∃x ∈ A, f(x) = y $$
It critically depend on its type signature, for example
q : N → N q(x) = x + 2 is not onto because no input map onto 0 or 1
Negating Onto:
$$ ¬∀y ∈ B, ∃x ∈ A, f(x) = y $$
or
$$ ∃y ∈ B, ∀x ∈ A, f(x) \neq y $$
if we want to show that f is not onto, we need to find some value y in B, such that no matter which element x you pick from A, f(x) isn’t equal to y.
Nested quantifiers
When quantifiers are nested, the meaning of the statement depends on the order of the two quantifiers.
For every person p in the Fleck family, there is a toothbrush t such that p brushes their teeth with t.
$$ \neq $$
There is a toothbrush t, such that for every person p in the Fleck family, p brushes their teeth with t.
- order issued when the statement is mixture of existential and universal quantifiers
Composing
$$ (g \circ f)(x)=g(f(x)) $$
- the declared domains and co-domains of the two functions aren’t all the same, so often you can only compose in one order
Terminology
function: map
onto: subjective
Image: $Im(f)$
range: refer to image or the co-domain, avoid using it
Proving
Define the function g from the integers to the integers by the formula g(x) = x − 8. g is onto.
- state the definition of onto: We need to show that for every integer y, there is an integer x such that g(x) = y.
- assign value: So, let y be some arbitrary integer. Choose x to be (y + 8).
- state x is integer: x is an integer, since it’s the sum of two integers
- state g(x) = y: g(x) = (y + 8) − 8 = y
- conclusion: so we’ve found the required pre-image for y and our proof is done
Let f : $\mathbb{Z}^2$→ Z be defined by f(x, y) = x + y. I claim that f is onto.
Let y be an element of Z. Then (0, y) is an element of f : $Z^2$and f(0, y) = 0 + y = y. Since this construction will work for any choice of y, we’ve shown that f is onto
For any sets A, B, and C and for any functions f : A → B and g : B → C, if f and g are onto, then g ◦ f is also onto.
- Let A, B, and C be sets. Let f : A → B and g : B → C be functions. Suppose that f and g are onto.
- We need to show that g ◦ f is onto. That is, we need to show that for any element x in C, there is an element y in A such that (g ◦ f)(y) = x.
- So, pick some element x in C. Since g is onto, there is an element z in B such that g(z) = x. Since f is onto, there is an element y in A such that f(y) = z.
- Substituting the value f(y) = z into the equation g(z) = x, we get g(f(y)) = x. That is, (g ◦ f)(y) = x. So y is the element of A we needed to find.
One to one
A function is one-to-one if it never assigns two input values to the same output value. Or, said another way, no output value has more than one preimage
$$ ∀x, y ∈ A, x \not = y → f(x) \not= f(y) $$
$$ ∀x, y ∈ A, f(x) = f(y) → x = y $$
pre image: Suppose that f : A → B is a function from A to B. If we pick a value y ∈ B, then x ∈ A is a pre-image of y if f(x) = y
prove
Let f : Z → Z be defined by f(x) = 3x + 7. f is one-to-one
Proof: We need to show that for every integers x and y, f(x) = f(y) → x = y. So, let x and y be integers and suppose that f(x) = f(y). We need to show that x = y. We know that f(x) = f(y). So, substituting in our formula for f, 3x + 7 = 3y + 7. So 3x = 3y and therefore x = y, by high school algebra. This is what we needed to show
Composition
For any sets A, B, and C and for any functions f : A → B and g : B → C, if f and g are one-to-one, then g ◦ f is also one-to-one
Strictly increasing functions
f is called strictly increasing if, for every x and y in A, x < y implies that f(x) < f(y)
For all strictly increasing functions, they are one-to-one function
Bijections
A function that is both one-to-one and onto is called bijective or a bijection
Inverse function: represent by $f^{-1}$. If f maps from A to B, then $f^{-1}$ maps from B to A.
Pigeonhole Principle
Suppose you have n objects and assign k labels to these objects. If n > k, then two objects must get the same label.
Among the first 100 powers of 17, there are two (distinct) powers which differ by a multiple of 57
Permutations
an ordered choice of k objects from a set of n objects is known as a k-permutation of the n objects. There are
$$ n(n-1)...(n-k+1)=\frac{n!}{(n-k)!} $$
different k-permutations of n objects, which is called P(n,k), which is also the number of one-to-one functions from a set of k objects to a set of n objects.
exception
$J = (a, p, p, l, e, t, r, e, e, s)$, we have 10! way to arrange. However, there are two duplicate possible which are p and e, to remove the exception, we do dividing
$$ \frac{10!}{2!3!} $$